反向传播

反向传播(BackPropagation)

关于反向传播

反向传播算法（Backpropagation，简称BP）的核心思想：反向传播是一种用于高效计算神经网络中损失函数相对于所有权重参数梯度的算法。它的名字来源于其计算过程：误差从输出层开始，逐层向后（反向）传播。为什么需要反向传播?神经网络通过梯度下降法来学习（更新权重）。为了更新权重$W$我们需要知道梯度$\frac{\partial \text{Loss}}{\partial W}$。它的核心目的是高效地计算损失函数相对于每一个权重的梯度（即导数）。有了这些梯度，我们就可以使用梯度下降等优化算法来更新权重，使得网络的输出更接近真实值。

关于权重

简单来说，权重决定了输入信号的重要性、方向和强度，是神经网络学习和表达复杂关系的核心参数。

1. 数学视角：线性变换的“斜率”与“方向”

在最基本的神经元模型中，一个神经元的输出是其所有输入的加权和，再经过一个激活函数。

$$ z = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b $$

$$ a = f(z) $$

单个权重的作用：权重$w_i$ 就像是线性函数 $y = wx + b$ 中的 $w$（斜率）。它控制了输入特征 $x_i$ 对后续计算的影响程度和方向。

权重集合的作用：所有权重构成一个权重向量 $W$（或者权重矩阵）。这个向量定义了在高维空间中的一个方向。前向传播中的 $ \mathbf{ z = W x + b} $ 这个操作，本质上是执行了一次线性变换，将输入数据$ x$ 投射到一个新的方向（由 $W$ 定义）上，以便后续进行非线性分割。

2. 几何视角：划分空间的“边界”

场景：假设我们在对一个二维数据集（包含特征$x_1$和$x_2$）进行二分类。

神经元的计算：$z=w_1x_1+w_2x_2+b$
激活函数：阶跃函数或Sigmoid函数。

这个方程 $w_1 x_1 + w_2 x_2 + b = 0 $ 在二维平面上定义了一条直线（决策边界）。权重 $( w_1 , w_2 ) $的作用：它们是这条直线的法向量。这个向量的方向垂直于决策边界，指向了模型认为的“正类”区域。偏置 $b$的作用：决定了决策边界离原点的距离。

对于更复杂的网络：

隐藏层中的每个神经元都通过其权重定义了一条这样的决策边界。
多个神经元的组合（即多层网络）可以创建多条边界，这些边界可以组合成复杂、非线性的决策区域（如多边形、曲线形）。
因此，权重集合共同定义了如何扭曲和划分输入空间，以使得不同类别的数据点能够被有效地分离。

3. 生物学视角：神经连接的“强度”

神经网络最初受到大脑的启发。

神经元：模仿大脑中的神经细胞。
连接（ synapses ）：模仿神经元之间的连接。
权重：模仿这些连接的强度。

一个权重值高，就像两个神经元之间有一条强壮、高效的连接，信号可以轻松通过，影响巨大。一个权重值低（或为负），就像连接很弱（或具有抑制性），信号难以通过，影响很小。学习的过程，就是根据经验不断调整这些连接强度的过程。

4. 学习/优化视角：模型的“可调旋钮”

在机器学习中，我们的目标是找到一个函数 $f$，它能最好地映射输入 $X$ 到输出 $Y$。神经网络提供了一个非常灵活的函数家族 $f ( X ; W , b )$，其中 $W $和 $b$ 就是参数。

权重是模型的参数：它们是模型在训练过程中需要学习和优化的变量。
训练过程：通过反向传播算法计算损失函数相对于每个权重的梯度$ \frac{\partial L}{\partial W} $，然后使用梯度下降法来更新权重：

$$ w^{\text{new}} = w^{\text{old}} - \eta \frac{\partial L}{\partial w} $$

权重的作用演变：在训练开始时，权重通常被随机初始化。随着训练的进行，每个权重都会根据其在减少总体预测误差中的“责任”被精细地调整。最终，一套训练好的权重就编码了从数据中学到的“知识”和“规律”。

一个简单的神经网络模型

为了说明过程，我们使用一个极其简单的三层网络：

输入层（2个神经元）：$x_1,x_2$（可认为样本有2个特征）
隐藏层（2个神经元）：$h_1,h_2$，使用Sigmoid激活函数$\sigma(z)=\frac{1}{1+e^{-z}}$
输出层（1个神经元）：$\hat{y}$，使用Sigmoid激活函数。
真实标签：$y$
损失函数：均方误差（MSE）$L=\frac{1}{2}(y-\hat{y})^2$ （这里的 $\frac{1}{2}$ 是为了求导时消去系数，简化计算）
每个神经元都带有偏置项。
符号说明：

$w$代表权重 (weight)，上标表示层数，下标表示连接。例如，$w_{11}^1$表示从输入层第1个神经元到隐藏层1第1个神经元的权重。
$b$代表偏置 (bias)，上标表示层数。例如，$b_1^1$表示隐藏层1第1个神经元的偏置。
$z$代表线性计算结果 (未经过激活函数)。上标和下标的含义与$w$类似。
$a$代表激活后的结果 (经过激活函数)。上标和下标的含义与$w$类似。
$L$代表损失函数 (Loss Function)。这里使用均方误差（MSE）

网络结构图如下：

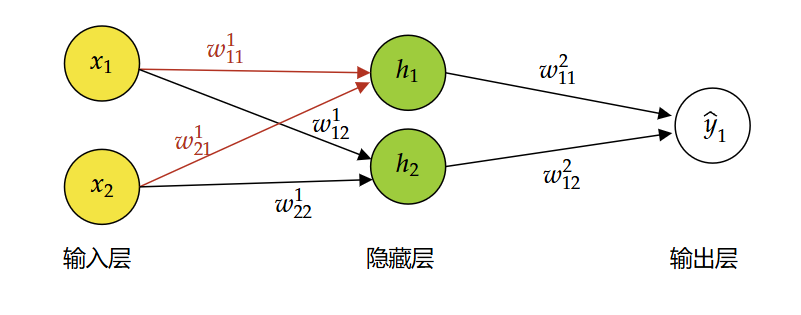
1. 前向传播(Forward Propagation)

首先，我们进行前向传播，计算预测值$\hat{y}$和损失$L$

1.1 从输入层到隐藏层：

权重和偏置

$$W^1 = \begin{bmatrix} w_{11}^1 & w_{12}^1 \\ w_{21}^1 & w_{22}^1 \end{bmatrix} \quad (2\times 2)$$

$$ B^1 = \begin{bmatrix} b_1^1 \\ b_2^1 \end{bmatrix} \quad (2 \times 1)$$

输入层到隐藏层的权重矩阵的大小：行 = 隐藏层的神经元数量，列=特征矩阵X的特征数量。

所有偏置矩阵是一个列向量，它的大小是权重链接的相邻两层中下一层的神经元数量。

未经过激活函数的输出(在计算结果的后面的括号内标注矩阵的大小，形式为$(\text{行数} \times \text{列数})$)

$$ z^1 = W^1 \cdot X^T + B^1 = \begin{bmatrix} w_{11}^1 & w_{12}^1 \\ w_{21}^1 & w_{22}^1 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} b_1^1 \\ b_2^1 \end{bmatrix} \qquad \mathbf{(1)}$$

$$ z^1 = \begin{bmatrix} w_{11}^1\cdot x_1 + w_{12}^1\cdot x_2 + b_1^1 \\ w_{21}^1\cdot x_1 + w_{22}^1\cdot x_2 + b_2^1 \end{bmatrix} = \begin{bmatrix} z_{1}^1 \\ z_{2}^1 \end{bmatrix} \quad (2\times 1) \qquad \mathbf{(2)}$$

$W\cdot X^T$表示两个矩阵相乘,$X^T$表示输入特征矩阵$x$的转置矩阵。

经过激活函数的输出

$$ a^1 = \sigma(z^1) = \begin{bmatrix} \sigma(w_{11}^1\cdot x_1 + w_{12}^1\cdot x_2 + b_1^1) \\ \sigma(w_{21}^1\cdot x_1 + w_{22}^1\cdot x_2 + b_2^1) \end{bmatrix} = \begin{bmatrix} a_{11}^1 \\ a_{21}^1 \end{bmatrix} \quad (2\times 1) \qquad \mathbf{(3)} $$

1.2 从隐藏层到输出层：

权重和偏置(

$$W^2 = \begin{bmatrix} w_{11}^2 & w_{12}^2 \end{bmatrix} \quad (1\times 2)$$

$$ B^2 = \begin{bmatrix} b_1^2 \end{bmatrix} \quad (1 \times 1) $$

注意，从第2层开始,也就是从隐藏层开始，权重的尺寸的行等于相邻两层下一层的神经元数量，列等于相邻两层上一层结果结果输出的行。

未经过激活函数的输出

$$ z^2 = W^2 \cdot a^1 + B^2 = \begin{bmatrix} w_{11}^2 & w_{12}^2 \end{bmatrix} \cdot \begin{bmatrix} a_{11}^1 \\ a_{21}^1 \end{bmatrix} + \begin{bmatrix} b_1^2 \end{bmatrix} \qquad \mathbf{(4)}$$

$$ z^2 = \begin{bmatrix} w_{11}^2 \cdot a_{11}^1 + w_{12}^2 \cdot a_{21}^1 + b_1^2 \end{bmatrix} \quad (1\times 1) \qquad \mathbf{(5)}$$

经过激活函数的输出

$$ a^2 = \sigma(z^2) = \sigma (w_{11}^2 \cdot a_{11}^1 + w_{12}^2 \cdot a_{21}^1 + b_1^2) = \hat{y}$$

1.3 计算损失:

$$ L = \frac{1}{2} (y - \hat{y})^2 = \frac{1}{2}(y-a^2)^2 $$

至此，前向传播完成，得到预测值$\hat{y} = a^2$和损失$L$

2. 反向传播(Back Propagation)

核心思想：链式法则。我们从输出层开始，逐层向后计算损失函数对每个权重和偏置的梯度（偏导数），然后用梯度下降法更新参数。具体来说，我们的目标是计算损失 $L$ 对于每个参数$w_{11}^1,w_{12}^1\cdots w_{11}^2, w_{12}^2 \dots, b_1^1 \dots, b_1^2$的的梯度，例如：$\frac{\partial L}{\partial w_{11}^2}$，我们将使用链式法则从后往前一步步推导。我们先从离损失最近的参数开始计算。

步骤 1：计算输出层权重的梯度$ \begin{bmatrix} w_{11}^2 & w_{12}^2 \end{bmatrix} \quad (1\times 2)$

我们想求$\frac{\partial L}{\partial w_{11}^2} $

$$ \frac{\partial L}{\partial w_{11}^2} = \frac{\partial L}{\partial a^2} \cdot \frac{\partial a^2}{\partial z^2} \cdot \frac{\partial z^2}{\partial w_{11}^2} $$

$ \frac{\partial L}{\partial a^2} = \frac{\partial}{\partial a^2}[\frac{1}{2}(y-a^2)^2] = -(y - a^2)$
$ \frac{\partial a^2}{\partial z^2}$，因为：$a^2 = \sigma(z^2) $，而$\sigma(z)$函数的导数$\sigma'(z) = \frac{d}{dz}(\frac{1}{1+e^{-z}}) = \frac{e^{-z}}{(1+e^{-z})^2} = \frac{e^{-z}}{(1+e^{-z})\cdot (1+e^{-z})} = \frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}} = \frac{1}{1+e^{-z}} \cdot \left( \frac{1+e^{-z}}{1+e^{-z}} - \frac{1}{1+e^{-z}}\right) = \sigma(z)(1-\sigma(z))$

而 $ \frac{\partial a^2}{\partial z^2}$相当于$a$对$z$求导数，所以：$\frac{\partial a^2}{\partial z^2} = a^2(1-a^2)$

$\frac{\partial z^2}{\partial w_{11}^2}$，由等式$\mathbf{(5)}$得到：$z^2 = w_{11}^2a_{11}^1 + w_{12}^2a_{21}^1 + b_1^2$，所以 $\frac{\partial z^2}{\partial w_{11}^2} = a_{11}^1$

将它们组合起来：

$$ \frac{\partial L}{\partial w_{11}^2} = [-(y-a^2)]\cdot [a^2(1-a^2)] \cdot a_{11}^1$$

为了简化，我们定义一个非常重要的概念：误差项$\delta$，定义输出层的误差项$\delta_o$，因为这里的输出层是$z^2$(未经过激活函数的输出)，所以

$$ \delta_o = \delta_{z^2} = \frac{\partial L}{\partial z^2} = \frac{\partial L}{\partial a^2} \cdot \frac{\partial a^2}{\partial z^2} = [-(y-a^2)]\cdot [a^2(1-a^2)] \qquad \mathbf{(6)}$$

有了输出层的误差$\delta_{z^2}$,那么输出层的权重梯度计算变成：

$$ \frac{\partial L}{\partial w_{11}^2} = \delta_{z^2} \cdot a_{11}^1 $$

$$ \frac{\partial L}{\partial w_{12}^2} = \delta_{z^2} \cdot a_{21}^1 $$

我们可以看出，输出层的权重梯度等于输出层的误差乘以上一层的激活输出$a^1$,但是输出层的权重是一个$(1\times 2)$矩阵，而上一层的激活输出$a^1$是一个$(2 \times 1)$矩阵。所以上面两个表达式可以合并写成：

$$ \frac{\partial L}{\partial W^2} = \delta_{z^2}\cdot (a^1)^T $$

输出层的偏置梯度：

$$ \frac{\partial L}{\partial b_{1}^2} = \frac{\partial L}{\partial a^2} \cdot \frac{\partial a^2}{\partial z^2} \cdot \frac{\partial z^2}{\partial b_{1}^2} = \delta_{z^2} \iff \left( \because \frac{\partial z^2}{\partial b_{1}^2} = 1 \right) $$

注意第2层输出就是输出层$\hat{y}$，只有一个输出节点，所以$\delta_{z^2}$没有下标。

步骤 2：计算输入层到隐藏层权重的梯度$ \begin{bmatrix} (w_{11}^1 & w_{12}^1 \\ w_{21}^1 & w_{22}^1) \end{bmatrix} (2 \times 2) $

现在我们向后一步，计算$\frac{\partial L}{\partial w^1}$。路径更长，链式法则也更长：

$$ \frac{\partial L}{\partial w^1} = \frac{\partial L}{\partial a^1} \cdot \frac{\partial a^1}{\partial z^1} \cdot \frac{\partial z^1}{\partial w^1} $$

根据公式$ \mathbf{(2),(3)}: a^1 = \begin{bmatrix} a_{11}^1 \\ a_{21}^1 \end{bmatrix}, z^1 = \begin{bmatrix} z_{1}^1 \\ z_{2}^1 \end{bmatrix}$ 该公式可分解成：

$$ \frac{\partial L}{\partial w_{11}^1} = \frac{\partial L}{\partial a_{11}^1} \cdot \frac{\partial a_{11}^1}{\partial z_{1}^1} \cdot \frac{\partial z_{1}^1}{\partial w_{11}^1} $$

$$ \frac{\partial L}{\partial w_{12}^1} = \frac{\partial L}{\partial a_{11}^1} \cdot \frac{\partial a_{11}^1}{\partial z_{1}^1} \cdot \frac{\partial z_{1}^1}{\partial w_{12}^1} $$

$$ \frac{\partial L}{\partial w_{21}^1} = \frac{\partial L}{\partial a_{21}^1} \cdot \frac{\partial a_{21}^1}{\partial z_{2}^1} \cdot \frac{\partial z_{2}^1}{\partial w_{21}^1} $$

$$ \frac{\partial L}{\partial w_{22}^1} = \frac{\partial L}{\partial a_{21}^1} \cdot \frac{\partial a_{21}^1}{\partial z_{2}^1} \cdot \frac{\partial z_{2}^1}{\partial w_{22}^1} $$

$ \frac{\partial z_{1}^1}{\partial w_{11}^1} = \frac{\partial}{\partial w_{11}^1} \left( w_{11}^1x_1 + w_{12}^1x_2 + b_1^1\right) = x_1, \frac{\partial z_{1}^1}{\partial w_{12}^1} = x_2, \frac{\partial z_{2}^1}{\partial w_{21}^1} = x_1, \frac{\partial z_{2}^1}{\partial w_{22}^1} = x_2$
$ \frac{\partial a_{11}^1}{\partial z_{1}^1} = \frac{\partial }{\partial z_{1}^1}(\sigma(z_{1}^1)) = a_{11}^1(1-a_{11}^1), \frac{\partial a_{21}^1}{\partial z_{2}^1} = a_{21}^1(1-a_{21}^1) $
难点在于计算$ \frac{\partial L}{\partial a^1} $

$$ \frac{\partial L}{\partial a_{11}^1} = \frac{\partial L}{\partial z^2} \cdot \frac{\partial z^2}{\partial a_{11}^1} $$

$$ \frac{\partial L}{\partial a_{21}^1} = \frac{\partial L}{\partial z^2} \cdot \frac{\partial z^2}{\partial a_{21}^1} $$

由公式$\mathbf{(5),(6)}$得到到：

$$ \frac{\partial z^2}{\partial a_{11}^1} = w_{11}^2, \quad \frac{\partial z^2}{\partial a_{21}^1} = w_{12}^2 $$

$$ \therefore \frac{\partial L}{\partial a_{11}^1} = \frac{\partial L}{\partial z^2} \cdot \frac{\partial z^2}{\partial a_{11}^1} = \delta_{z^2} \cdot w_{11}^2$$

$$ \therefore \frac{\partial L}{\partial a_{21}^1} = \frac{\partial L}{\partial z^2} \cdot \frac{\partial z^2}{\partial a_{21}^1} = \delta_{z^2} \cdot w_{12}^2$$

现在我们可以写出$\frac{\partial L}{\partial w_{11}^1}、\frac{\partial L}{\partial w_{12}^1}、\frac{\partial L}{\partial w_{21}^1}、\frac{\partial L}{\partial w_{22}^1}$完整的公式：

$$ \frac{\partial L}{\partial w_{11}^1} = \frac{\partial L}{\partial a_{11}^1} \cdot \frac{\partial a_{11}^1}{\partial z_{1}^1} \cdot \frac{\partial z_{1}^1}{\partial w_{11}^1} = (\delta_{z^2}\cdot w_{11}^2)(a_{11}^1(1-a_{11}^1)) \cdot x_1$$

$$ \frac{\partial L}{\partial w_{12}^1} = \frac{\partial L}{\partial a_{11}^1} \cdot \frac{\partial a_{11}^1}{\partial z_{1}^1} \cdot \frac{\partial z_{1}^1}{\partial w_{12}^1} = (\delta_{z^2}\cdot w_{11}^2)(a_{11}^1(1-a_{11}^1)) \cdot x_2$$

$$ \frac{\partial L}{\partial w_{21}^1} = \frac{\partial L}{\partial a_{21}^1} \cdot \frac{\partial a_{21}^1}{\partial z_{2}^1} \cdot \frac{\partial z_{2}^1}{\partial w_{21}^1} = (\delta_{z^2}\cdot w_{12}^2)(a_{21}^1(1-a_{21}^1)) \cdot x_1$$

$$ \frac{\partial L}{\partial w_{22}^1} = \frac{\partial L}{\partial a_{21}^1} \cdot \frac{\partial a_{21}^1}{\partial z_{2}^1} \cdot \frac{\partial z_{2}^1}{\partial w_{22}^1} = (\delta_{z^2}\cdot w_{12}^2)(a_{21}^1(1-a_{21}^1)) \cdot x_2$$

同样，我们定义隐藏层($z^1$)的误差项$\delta_{z^1}$：

$$ \delta_{z^1} = \frac{\partial L}{\partial z^1} = \frac{\partial L}{\partial a^1} \cdot \frac{\partial a^1}{\partial z^1} = (\delta_{z^2} \cdot w^2)(a^1(1-a^1))$$

隐藏层的偏置梯度:

$$ \frac{\partial L}{\partial b^1} = \frac{\partial L}{\partial a^1} \cdot \frac{\partial a^1}{\partial z^1} \cdot \frac{\partial z^1}{\partial b^1} = \delta_{z^1}$$

于是

$$\frac{\partial L}{\partial w^1} = \delta_{z^1} \cdot x $$

反向传播通用计算公式

1. 基本符号定义

$L$：损失函数
$z^{(l)}$：第$l$层的加权输入(未经激活函数的输入)
$a^{(l)}$：第$l$层的激活输出(经激活函数的输出)
$W^{(l)}$：第$l-1$层到$l$层权重矩阵
$b^{(l)}$：第$l$层偏置向量
$f^{(l)}$：第$l$层的激活函数
$f^{(l)'}$：激活函数的导数
$\delta^{(l)}$：第$l$层的误差，$\delta^{L}$表示输出层误差。对于$l=L-1,L-2,\cdots,2$

2. 通用前向传播公式

$$ z^{l} = W^{(l)}a^{(l-1)} + b^{(l)}$$

$$ a^{l} = f^{(l)}(z^{(l)})$$

当$l=1$是, $a^{(0)}$表示输入特征本身。

3. 通用反向传播公式

输出层误差项

$$ \delta^{L} = \frac{\partial L}{\partial z^{(L)}} = \nabla_{a^{(L)}} L \odot f^{(L)'}(z^{(L)}) $$

其中$\nabla_{a^{(L)}}L$是损失对输出层激活值的导数,在上面的例子中，就是$\frac{\partial L}{\partial a^2} = -(y-a^2) = -(y-\hat{y})，f^{(L)'}(z^{(L)})$就是输出层激活输出对于输入的导数。上面的例子中就是$\frac{\partial a^2}{\partial z^2} = a^2(1-a^2) = \hat{y}(1-\hat{y})$

隐藏层误差项

$$ \delta^{l} = \frac{\partial L}{\partial z^{(l)}} = \left( (W^{(l+1)})^T \delta^{(l+1)} \right) \odot f^{(l)'}(z^{(l)}) $$

权重梯度

$$ \frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} (a^{(l-1)})^T$$

当$l-1=0$时表示输入数据本身。

$$ \frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} (X)^T$$

偏置梯度

$$\frac{\partial L}{b^{(l)}} = \delta{(l)}$$

几个常用的激活函数

1. Sigmoid

$$ a = \sigma(z) = \frac{1}{1+e^{-z}} $$

$$ \sigma'(z) = \frac{1}{1+e^{-z}} \cdot \left(1 - \frac{1}{1+e^{-z}}\right) = \sigma(z) \cdot (1-\sigma(z))$$

2. Tanh

$$ a = \tanh(z) = \frac{e^{z} - e^{-z}}{e^z + e^{-z}}= \frac{e^{2z} - 1}{e^{2z}+1} $$

$$ \tanh'(z) = \frac{1}{\cosh^2(z)}$$

$$ \because \cosh(x) = \frac{e^x + e^{-x}}{2} \quad \therefore \tanh'(z) = \frac{4}{(e^z+e^{-z})^2} = 1 - \left( \frac{e^{2z}-1}{e^{2z}+1}\right)^2 = 1 - \tanh^2(z) $$

3. Softmax

Softmax作为输出层的激活函数，一般用于多分类的设计。

$$ \text{Softmax}(z_i) = \frac{e^{z_i}}{\displaystyle{\sum_{j=1}^C e_{z_j}}} $$

其中$C$是类别总数（也是输出层神经元数量）。举例：假设一个3分类问题，输出层3个神经元，对于某个样本，它们原始的logits(如Sigmoid)输出是 [2.0, 1.0, 0.1]。

计算总和:

$$ e^{2.0} + e^{1.0} + e^{0.1} \approx 7.39 + 2.72 + 1.1 \approx 11.22 $$

计算每个类别的概率：

$$ \begin{array}{l} p_0 = \frac{7.39}{11.22} \approx 0.66 \\ p_1 = \frac{2.72}{11.22} \approx 0.24 \\ p_2 = \frac{1.1}{11.22} \approx 0.1 \end{array} $$

最终输出概率向量：[0.66, 0.24, 0.10]。模型会预测该样本属于类别0。

交叉熵损失（Cross-Entropy Loss）

与Softmax输出层配对使用的标准损失函数是分类交叉熵。它衡量的是模型输出的概率分布与真实的概率分布之间的“距离”。在分类问题中，真实分布是“一位有效”的形式。对于上面的3分类例子，如果该样本的真实标签是“类别1”，那么它的One-hot标签就是 [0, 1, 0]。交叉熵损失公式：

$$ L = -\sum_{i=1}^C y_i \log(p_i) = -\sum_{i=1}^C y_i \log(a_i)$$

其中:$C:$类别总数, $y_i:$真实标签在第 $i$ 个类别上的值（0或1）。$p_i:$模型预测的第 $i$ 个类别的概率。接上例：真实标签 y = [0, 1, 0],预测概率 p = [0.66, 0.24, 0.10]，损失计算：

$$ L = - (0 * \log(0.66) + 1 * \log(0.24) + 0 * \log(0.10)) = - \log(0.24) ≈ 1.427 $$

损失函数的直观理解：

当模型预测的概率 $p_i$ 对真实类别非常自信（接近1）时，$-\log(p_i)$ 会非常小（接近0）。
当模型预测错误或不确定时（概率远离1），$-\log(p_i)$ 会很大。
因此，训练过程就是通过反向传播和梯度下降，最小化这个交叉熵损失，从而调整网络所有权重，使得模型对真实类别的预测概率尽可能接近1。

反向传播

由于Softmax和交叉熵在数学上的紧密结合，当它们一起使用时，损失函数对于输出层原始logits (z) 的梯度会变得非常简单和优雅：

$$ \frac{\partial L}{\partial z_i} = p_i - y_i = a_i^o - y_i $$

$a_i^o$是输出层预测输出，$y_i$是真实标签值

QkCalc中的反向传播

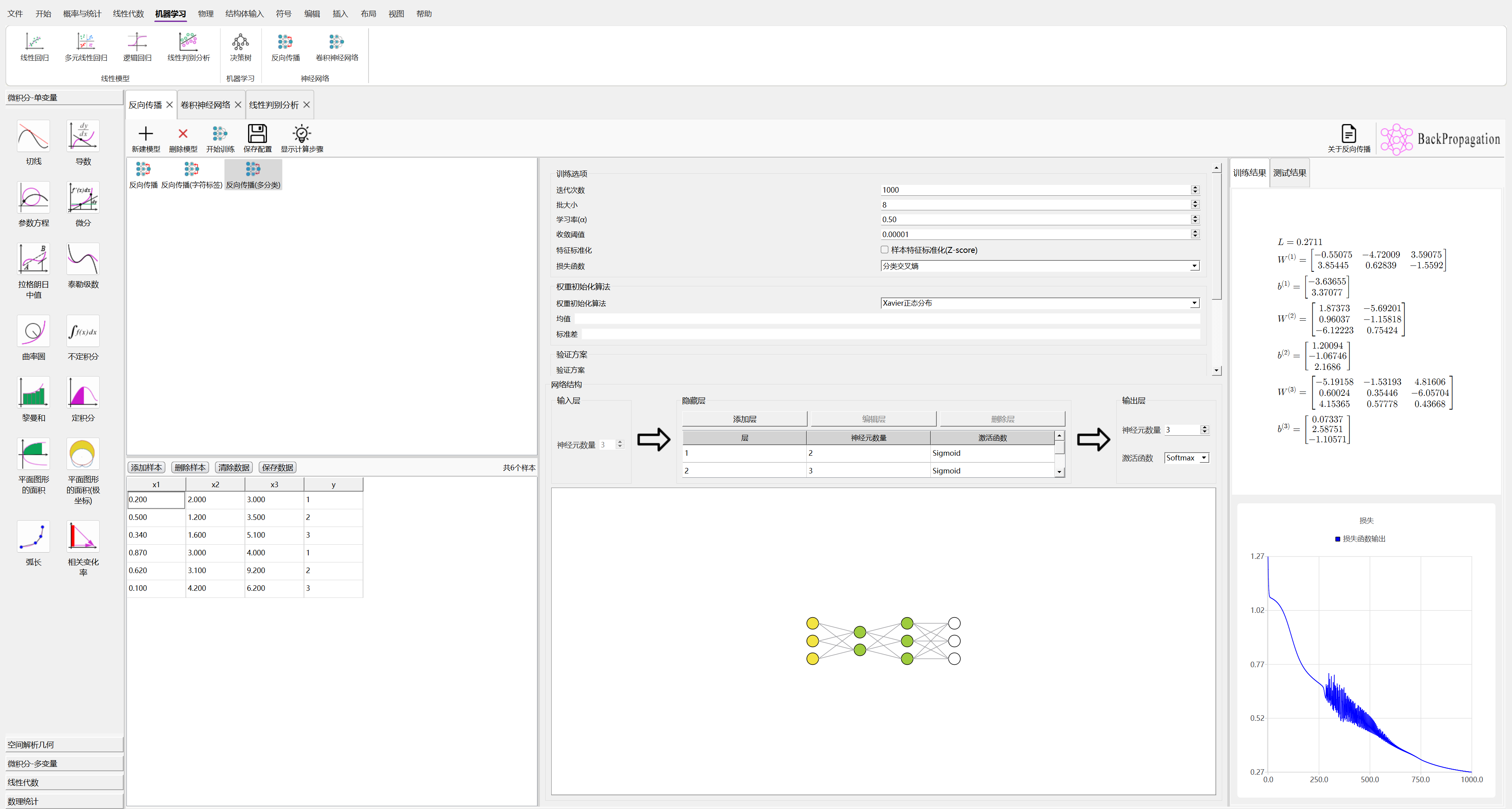
在QkCalc你可以快速建立反向传播算法模型，设定训练参数，包括：误差函数、激活函数，通过图形化方式定义神经网络结构，查看可视化的训练结果和损失的收敛。