LSTM-长短时记忆网络

LSTM（Long Short-Term Memory，长短时记忆网络）

关于LSTM

LSTM（Long Short-Term Memory，长短时记忆网络）是一种特殊的循环神经网络（RNN），由Sepp Hochreiter和Jürgen Schmidhuber于1997年提出，专门设计用来解决传统RNN在处理长序列时遇到的梯度消失/爆炸问题。

核心特点与优势

记忆长依赖关系：能够学习并记住数百步之前的输入信息
门控机制：通过精密的门控系统控制信息的流动
梯度稳定性：有效缓解了训练过程中的梯度问题

核心结构：三个门控制单元

LSTM的核心是细胞状态（Cell State），像一条“传送带”，贯穿整个时间序列。通过三个门控制信息的流动：

1.遗忘门（Forget Gate）：决定从细胞状态中丢弃哪些信息

$$ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) $$ $\sigma$为Sigmoid函数，输出0-1之间的值；$W_f$为遗忘门的权重；$x_t$为当前时间步的输入；$h_{t-1}$为上一时刻的隐藏状态；$b_f$为遗忘门的偏置。注意，这里的

$$ [h_{t-1}, x_t] $$

是拼接操作，例如

$$ h_{t-1} = [0.2, 0.5, -0.1], x_t=[0.8, 0.3]， [h_{t-1}, x_t] = [0.2, 0.5, -0.1, 0.8, 0.3]$$

2. 输入门（Input Gate）：决定哪些新信息存储在细胞状态中

$$ i_t = \sigma(W_i \cdot [h_{t-1}, x_t]) + b_i$$

$$ \tilde{C}_t = \tanh(W_C\cdot[h_{t-1}, x_t] + b_C)$$

其中$W_i$为输入门的权重；$b_i$为输入门的偏置。$\tilde{C}_t$为候选记忆，它是基于当前输入和过去隐藏状态生成的新候选记忆内容。$b_C$是候选记忆的偏置。

3. 输出门（Output Gate）：决定从细胞状态输出什么信息

$$ o_t = \sigma(W_o\cdot[h_{t-1}, x_t] + b_o) $$

$$ h_t = o_t \odot \tanh(C_t) $$

$W_o$为输出门的权重，$b_o$为输出门的偏置。$h_t$当前隐藏层的输出。需要注意的是,$h_t$使用的逐元素相乘，也即是Hadamard product，哈达玛积

更新机制：细胞状态的更新公式：

$$ C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$$ $C_t$当前时刻的细胞状态，它等于 遗忘门 乘以 上一时刻的细胞状态 加上 当前输入门 乘以 当前候选记忆。 同样的$C_t$的计算也使用的逐元素相乘。

***LSTM的逐元素相乘是门控机制的核心，实现了信息的选择性流动这是LSTM相比RNN的主要创新之一：用门控（逐元素相乘）替代了直接覆盖。***

LSTM的工作流程：

$$ 输入 \rightarrow 遗忘门(决定忘记什么) \rightarrow 输入门(决定记住什么) \rightarrow 更新细胞状态 \rightarrow 输出门(决定输出什么) \rightarrow 隐藏状态输出$$

LSTM的网络结构图：

主要应用领域

自然语言处理：机器翻译、文本生成、情感分析
时间序列分析：股票预测、天气预测、设备故障预测
语音识别：语音转文本、语音合成
视频分析：动作识别、视频描述生成

优点与局限性

优点：

能够处理长序列依赖
门控机制使训练更稳定
在实践中表现优异

局限性：

参数较多，计算成本高
训练时间相对较长
可能过拟合，需要正则化

发展现状

虽然Transformer架构在某些任务上已经超越了LSTM，但LSTM仍然在许多实际应用中广泛使用，特别是在数据量较小或序列长度不是特别长的场景中，因其结构相对简单且在许多任务上仍有良好表现。 LSTM作为深度学习发展史上的重要里程碑，为序列建模任务奠定了坚实的基础，其设计思想至今仍在影响新模型架构的开发。

计算过程

一个超简化的计算举例

场景设定：假设我们有一个超简化的LSTM单元，其维度仅为1（所有向量都是标量），方便我们计算。我们处于时间步 $t$。

输入：当前输入$x_t = 0.8$
上一时刻的隐藏状态：$h_{t-1} = 0.5$
上一时刻的细胞状态：$ C_{t-1} = 1.2 $ 这是LSTM的“长期记忆”
权重和偏置：为了简化，我们假设所有权重 $W_f, W_i, W_C, W_o$ 都为 0.5，所有偏置 $b_f, b_i, b_C, b_o$ 都为 0.1。
激活函数：$\sigma$为Sigmoid，$\tanh$为双曲正切。

第一步：计算遗忘门

公式：$$ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)$$

$$ f_t = \sigma(0.5 \times [0.5, 0.8] + 0.1) = \sigma(0.5\times 0.5 + 0.5 \times 0.8 + 0.1) = \sigma(0.75) $$

$$ \sigma(0.75) = \frac{1}{1+e^{-0.75}} \approx 0.679 $$

所以 $f_t \approx 0.679 $表示我们打算保留大部分（约68%）的上一时刻细胞状态，遗忘约32%。

第二步：计算输入门 $i_t$ 和候选记忆 $ \tilde{C}_t$

A 输入门

$$ i_t = \sigma(W_i \cdot [h_{t-1}, x_t]) + b_i$$

$$ i_t = \sigma(0.5 \times [0.5, 0.8] + 0.1) = \sigma(0.5\times 0.5 + 0.5 \times 0.8 + 0.1) = \sigma(0.75) \approx 0.679 $$

所以，$i_t \approx 0.679 $。表示我们打算让约68%的新信息加入记忆。

B 候选记忆$\tilde{C}_t$公式：

$$ \tilde{C}_t = \tanh(W_C\cdot[h_{t-1}, x_t] + b_C)$$

$$ \tilde{C}_t = \tanh(0.5 \times [0.5, 0.8] + 0.1) = \tanh(0.75) $$

$$ \tanh(0.75) = \frac{e^{0.75} - e^{-0.75}}{e^{0.75} + e^{-0.75}} \approx 0.635 $$

所以，$\tilde{C}_t ≈ 0.635$。这是基于当前输入和过去隐藏状态生成的新候选记忆内容。

第三步：更新细胞状态$C_t$

这是LSTM的核心步骤，我们结合“遗忘”和“输入”来更新长期记忆。公式：

$$ C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$$

1. $ f_t \cdot C_{t-1} = 0.679 \times 1.2 \approx 0.815 $ (这是保留的旧记忆)

2. $ i_t \cdot \tilde{C}_t = 0.679 \times 0.635 \approx 0.431 $ (这是要添加的新记忆)

$$C_t = 0.815 + 0.431 = 1.246$$

所以，新的长期记忆 $C_t \approx 1.246$。可以看到，它从原来的 1.2 更新为了 1.246，结合了旧信息和新信息。

第四步：计算输出门 $o_t$ 和当前隐藏状态 $h_t$

输出门决定基于当前的细胞状态，我们要输出多少信息到隐藏状态（即短期记忆/上下文信息）。

A 输出门

$$ o_t = \sigma(W_o\cdot[h_{t-1}, x_t] + b_o) $$

$$ o_t = \sigma(0.5 \times [0.5, 0.8]) + 0.1) = \sigma(0.75) \approx 0.679 $$

所以，$o_t \approx 0.68$。表示我们打算输出约68%的当前细胞状态信息。

B. 当前隐藏状态

$$ h_t = o_t \odot \tanh(C_t) = 0.679 \times \tanh(1.246) \approx 0.575 $$

所以，当前隐藏状态 $h_t ≈ 0.575$。这个 $h_t$ 会作为LSTM单元在当前时间步的输出，并传递给下一个时间步，同时也会用于计算当前时间步的预测（如果需要）。这个时间步的计算就此完成。我们得到了：

新的长期记忆：$C_t = 1.25$

新的隐藏状态（输出）：$h_t = 0.58$

这个过程在下个时间步$ t+1$ 会完全重复。

LSTM的输出层

LSTM是一个序列处理器，它的主要任务是：

逐步处理输入序列
提取时序特征
生成包含整个序列信息的隐藏状态，例如上面新的隐藏状态$h_t$包含了序列的"理解"，但还不是分类结果。

下面详细解释为什么LSTM后面需要接分类层，以及LSTM和分类层的不同角色。

1. 分类任务的需求：

我们需要一个明确的决策：如：$$正面情感 \rightarrow 概率 0.85 \\\\ 负面情感 \rightarrow 概率 0.15$$

问题：LSTM的隐藏状态是高维特征向量，不是概率分布！

2. 为什么不能直接用LSTM的输出？

假设隐藏状态维度=128 $$ h_{\text{last}} = [0.34, -0.12, 0.89, \cdots, 0.56] \quad 128个值$$

而我们需要的是一个$0\sim 1$之间的概率值：

$$ \text{prob positive} = 0.85 \quad \text{prob negative} = 0.15 $$

三个主要问题：

问题1：维度不匹配：LSTM输出：128维特征向量，分类需要：2维概率向量（二分类）
问题2：值域不合适：LSTM隐藏状态：任意实数（如：tanh输出在(-1,1)），分类概率：需要在(0,1)之间且和为1
问题3：缺乏可解释的决策边界： LSTM学到的是特征表示，不是决策规则。

3. 分类层的具体作用

结构示意图：$$ 原始句子 \rightarrow 词向量 \rightarrow \text{LSTM} \rightarrow 最后隐藏状态 (特征提取器) \rightarrow 分类层 \rightarrow 情感概率(决策器) $$

4. 分类层的实现

分类层（通常就是全连接层 + Softmax），Softmax的作用：

归一化：确保所有类别概率和为1
概率解释：将分数转换为概率
放大差异：突出最高概率的类别

5. 分类层一定要含隐藏层吗？

不一定需要隐藏层！三种常见的分类层架构

直接投影（无隐藏层）
单隐藏层
多隐藏层

不同场景下的选择建议

简单任务，充足数据：无需隐藏层；复杂任务，中等数据：需要一个隐藏层；多任务或领域特定：多个隐藏层；

实验对比：有 vs 无隐藏层:

指标	无隐藏层	有隐藏层
参数数量	少	多
训练速度	快	慢
过拟合风险	低	高
特征组合能力	弱	强
适合任务复杂度	低	中高

反向传播计算过程（BPTT）

反向传播的目标是计算损失函数对所有权重参数的梯度，然后用梯度下降法更新参数。LSTM 的反向传播比普通 RNN 复杂，因为涉及细胞状态和三个门控。

1. LSTM前向传播总结：

输入拼接：$$ z_t = \begin{bmatrix} h_{t-1} \\ x_t \end{bmatrix} \in \mathbb{R}^{d_h + d_x}$$

遗忘门： $$ f_t = \sigma(W_fz_t + b_f)$$

输入门： $$ i_t = \sigma(W_iz_t + b_i)$$

候选细胞状态： $$ \tilde{C}_t = \tanh(W_Cz_t + b_C)$$

细胞状态更新： $$ C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$$

输出门： $$ o_t = \sigma(W_oz_t + b_o)$$

隐藏状态： $$ h_t = o_t \odot \tanh(C_t)$$

分类层(分类层)： $$ y = W_yh_t + b_y, \hat{y}_t = \text{Softmax}(W_yh_t + b_y) $$其中$W_y, b_y$分别是分类层的权重和偏置。

2. 梯度定义和反向传播总览

定义以下梯度：

$\delta W_y = \frac{\partial L}{\partial W_y}$: 分类层
$\delta h_t = \frac{\partial L}{\partial h_t}$: 隐藏状态的梯度
$\delta C_t = \frac{\partial L}{\partial C_t}$: 细胞状态的梯度
$\delta f_t = \frac{\partial L}{\partial f_t}$: 遗忘门的梯度
$\delta i_t = \frac{\partial L}{\partial i_t}$: 输入门的梯度
$\delta o_t = \frac{\partial L}{\partial o_t}$: 输出门的梯度
$\delta \tilde{C}_t = \frac{\partial L}{\partial \tilde{C}_t}$: 候选细胞状态的梯度

损失函数对于输出层的梯度 $$ \frac{\partial L}{\partial y}= \hat{y}_t - y_t $$

$$ \frac{\partial L}{\partial W_y} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial W_y} = (\hat{y}_t - y_t)h_t $$

$$ \frac{\partial L}{\partial b_y} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial b_y} = \hat{y}_t - y_t $$

$$ \frac{\partial L}{\partial h_T} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial h_T} = (\hat{y}_t - y_t)W_y $$

$h_T$是最后时间步的隐藏输出。

3. 沿时间反向传播（BPTT）

假设最后一个时间步$t = T$，假设$T=6$我们从最后一个时间步开始反向计算到$ t=1$。对于每个时间步，我们需要计算：

对当前隐藏状态 $h_t$ 的梯度
对当前细胞状态 $C_t$ 的梯度
对各个门控和参数的梯度

时间步 $t=6$ 的反向传播

已知：

来自分类层的梯度：$$ δ_{h6} = \frac{\partial L}{\partial h_T} $$
来自未来的梯度（t=6是最后一步，所以没有来自未来的梯度）

定义符号：

$\delta_{h_t} $：损失对 $h_t$ 的总梯度
$\delta_{C_t} $：损失对 $C_t$ 的梯度
$δ_{h_\text{next}}$ 和 $\delta_{C_\text{next}}$ 来自下一步（对 t=6 来说，这些为0）

$C_t$ 的梯度有两个来源：

通过 $h_t$：因为 $h_t = o_t \odot \tanh(C_t)$
直接流向下一步：因为 $C_t$ 会传给 $C_{t+1}$（对 t=6 没有下一步）

对于 $t=6$ 的具体计算：

回忆前向传播时：

$$ \begin{array}{l} h_6 = o_6 \odot \tanh(C_6) \\ o_6 = \sigma(z_{o_6}) \\ C_6 = f_6 \odot C_5 + i_6 \odot \tilde{C}_6 \\ \tilde{C}_6 = \tanh(z_{c_6}) \\ i_6 = \sigma(z_{i_6}) \\ f_6 = \sigma(z_{f_6}) \end{array}$$

其中：$ z_{o_6} = W_oz_6 + b_o，z_{c_6} = W_Cz_6 + b_C,z_{i_6} = W_iz_6 + b_i, z_{f_6} = W_fz_6 + b_f $

a) 计算 $\delta_{C_6}$：

$$ \frac{\partial h_6}{\partial C_6} = o_6 \odot (1 - \tanh(C_6)^2) \impliedby h_6 = o_6 \odot \tanh(C_6) \quad \because \tanh'(x) = 1-\tanh(x)^2$$

$$ \delta_{C_6} = \left( \frac{\partial L}{\partial h_6} \right) \odot \frac{\partial h_6}{\partial C_6} + \delta_{C_{\text{next}}} \quad \delta_{C_{\text{next}}} = 0 $$

b) 计算 $\delta_{o_6}$：

$$ \frac{\partial h_6}{\partial o_6} = \tanh(C_6) \impliedby h_6 = o_6 \odot \tanh(C_6) $$

$$ \delta_{o_6} = \frac{\partial L}{\partial h_6} \odot \frac{\partial h_6}{\partial o_6} = \delta_{h_6} \odot \tanh(C_6) $$

$$ \delta_{z_{o_6}} = \frac{\partial L}{\partial h_6} \odot \frac{\partial h_6}{\partial o_6} \odot \frac{\partial o_6}{\partial z_{o_6}} = \delta_{o_6} \odot \left(\sigma({z_{o_6}}) \odot (1-\delta({z_{o_6}}))\right) = \delta_{o_6} \odot [o_6 \odot (1-o_6)] $$

c) 计算 $\delta_{\tilde{C}_6}$：

$$ \frac{\partial C_6}{\partial \tilde{C}_6} = i_6 \impliedby C_6 = f_6 \odot C_5 + i_6 \odot \tilde{C}_6 $$

$$ \delta_{\tilde{C}_6} = \frac{\partial L}{\partial C_6} \odot \frac{\partial C_6}{\partial \tilde{C}_6} = \delta_{C_6} \odot i_6 $$

$$ \delta_{z_{c_6}} = \frac{\partial L}{\partial C_6} \odot \frac{\partial C_6}{\partial \tilde{C}_6} \odot \frac{\partial \tilde{C}_6}{\partial z_{c_6}} = \delta_{\tilde{C}_6} \odot i_6 \odot (1-\tilde{C}^2_6) $$

d) 计算 $\delta_{i_6}$：

$$ \frac{\partial C_6}{\partial i_6} = \tilde{C}_6 \impliedby C_6 = f_6 \odot C_5 + i_6 \odot \tilde{C}_6 $$

$$ \delta_{i_6} = \frac{\partial L}{\partial h_6} \odot \frac{\partial h_6}{\partial C_6} \odot \frac{\partial C_6}{\partial i_6} = \delta_{C_6} \odot \tilde{C}_6 $$

$$ \delta_{z_{i_6}} = \delta_{i_6} \odot \frac{\partial i_6}{\partial z_{i_6}} = \delta_{i_6} [i_6 \odot (1-i_6)] \impliedby i_6 = \sigma(z_{i_6}) $$

e) 计算 $\delta_{f_6}$（注意：$f_6$作用于$C_5$，所以梯度会传播到$C_5$）：

$$ \frac{\partial C_6}{\partial f_6} = C_5 \impliedby C_6 = f_6 \odot C_5 + i_6 \odot \tilde{C}_6 $$

$$ \delta_{f_6} = \delta_{C_6} \odot C_5 $$

$$ \frac{\partial f_6}{\partial z_{f_6}} = f_6 \odot (1-f_6) $$

$$ \delta_{z_f6} = \delta_{f_6}\odot \frac{\partial f_6}{\partial z_{f_6}} $$

f) 计算对$C_5$的梯度：：

$$ \frac{\partial C_6}{\partial C_5} = f_6 \impliedby C_6 = f_6 \odot C_5 + i_6 \odot \tilde{C}_6 $$

$$ \delta_{C_5 \text{from} t_6} = \delta_{C_6} \odot f_6$$

g) 计算对$h_5$的梯度：

所有门计算都依赖于拼接向量 $[h_5, x_6]$，所以梯度会流向 $h_5$。对于每个门控变量 $g \in {z_{f_6}, z_{i_6}, z_{c_6}, z_{o_6}}：$

$$ \frac{\partial g}{\partial h_5} = W_g[:, :h] \quad W_g的前h列 $$

所以$\delta_{h_5}$累积来自四个门的梯度：

$$ \delta_{h_{5_\text{total}}} = W_f[:,:2]^T \cdot \delta_{z_{f_6}} + W_i[:,:2]^T \cdot \delta_{z_{i_6}} + W_c[:,:2]^T \cdot \delta_{z_{c_6}} + W_o[:,:2]^T \cdot \delta_{z_{o_6}} + \delta_{h_{\text{next}}}（这里为0） $$

时间步 $t=5$ 到 $t=1$

重复上述过程，但要注意：

每个时间步的 $\delta_{h_t}$ 有两个来源：1) 来自下一步的 $\delta_{h_\text{next}}$，2) 来自当前步的梯度计算
每个时间步的 $\delta_{C_t}$ 有两个来源：1) 来自下一步的 $\delta_{C_\text{next}}$（通过遗忘门），2) 来自当前步通过 $h_t$ 的梯度

4. 反向传播（BPTT）通用公式

计算当前时间步的$\delta_{C_t}$

$$ \delta_{C_t} = \delta_{C_\text{next}} \odot f_{t+1} + (\delta_{h_t} \odot o_t \odot (1 - \tanh^2(C_t)))$$

计算各个门的梯度

$$ \delta_{z_{o_t}} = \delta_{h_t} \odot \tanh(C_t) \odot o_t (1 - o_t) $$

$$ \delta_{z_{i_t}} = \delta_{C_t} \odot \tilde{C}_t \odot i_t \odot (1-i_t) $$

$$ \delta_{z_{f_t}} = \delta_{C_t} \odot C_{t-1} \odot f_t \odot (1-f_t) $$

$$ \delta_{z_{c_t}} = \delta_{C_t} \odot i_t \odot (1 - \tilde{C}^2_t) $$

计算对前一步的梯度

$$ \delta_{h_{t-1}} = W_f[:, :h] \cdot \delta_{z_{f_t}} + W_i[:,:h] \cdot \delta_{z_{i_t}} + W_c[:, :h] \cdot \delta_{z_{c_t}} + W_o[:, :h] \cdot \delta_{z_{o_t}} $$

$$ \delta_{C_{t-1}} = \delta_{C_t} \odot f_t $$

5. 计算参数梯度

对于每个时间步 $t$，我们得到四个门的梯度$\delta_{z_{f_t}}, \delta_{z_{i_t}}, \delta_{z_{c_t}}, \delta_{z_{o_t}}$ ，对权重参数的梯度是各个时间步的累加：

$$ \frac{\partial L}{\partial W_f} = \sum_{t=1}^T[\delta_{z_{f_t} \cdot \text{concat}_t}]$$

$$ \frac{\partial L}{\partial b_f} = \sum_{t=1}^T \delta_{z_{f_t}} $$

其他权重同理。

6. 对输入词向量的梯度：

$$ \delta_{x_t} = W_f[:, h:] \cdot \delta_{z_{f_t}} + W_i[:,h:] \cdot \delta_{z_{i_t}} + W_c[:, h:] \cdot \delta_{z_{c_t}} + W_o[:, h:] \cdot \delta_{z_{o_t}}$$

注意，词向量取权重的后$d_x$列。这可以用来更新词向量（如果词向量是可训练的）。

如何确定词向量是可训练的？词向量的三种训练模式:

模式1：不可训练（静态词向量）
模式2：完全可训练
模式3：部分可训练（微调）

如何确定词向量是否可训练？

if 数据量小:
    使用预训练 + 冻结
elif 有高质量领域预训练:
    使用预训练 + 微调
elif 数据量大且领域特殊:
    从头训练
else:
    预训练 + 微调（最常用）

在QkCalc中设计LSTM

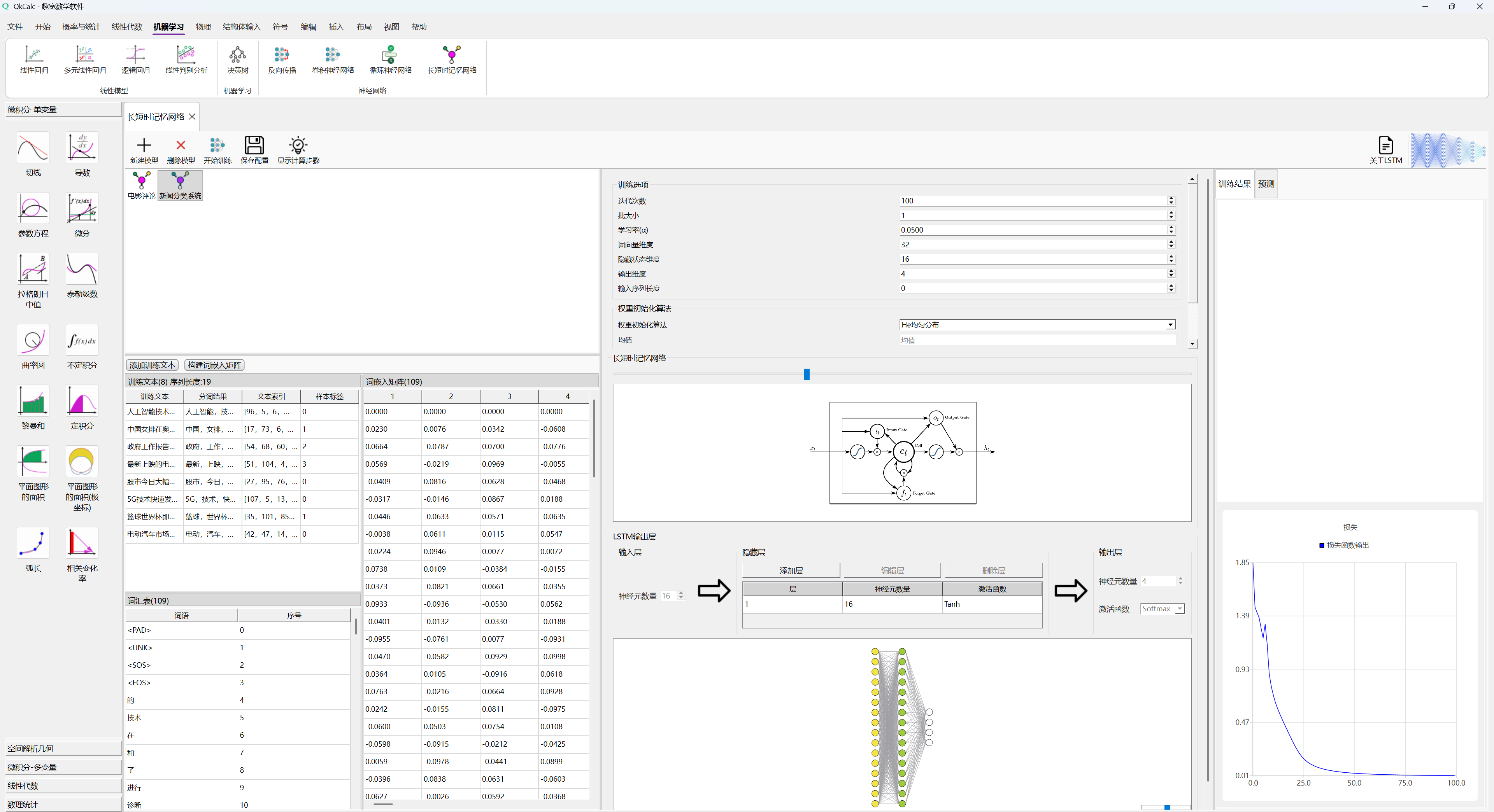
在QkCalc中，你可以通过“机器学习”中的“长短时记忆网络”来建立LSTM模型，通过设定参数、并可建立一个全连接层用于LSTM的输出层，通过快速生成词嵌入矩阵和样本进行训练和测试。