循环神经网络(Recurrent Neural Network)
关于RNN
RNN,即循环神经网络,是专门为处理序列数据而设计的一类神经网络。它的核心思想是引入“记忆”的概念,使网络能够利用之前步骤中的信息。
- 核心思想:具有“记忆”的神经网络
- 前馈神经网络(如MLP、CNN)的局限:它们假设所有的输入(和输出)是相互独立的。你输入一个数据点,它给出一个结果,这个结果不会影响下一个数据点的处理。这对于图像分类很有效,但对于理解句子、语音等序列数据就力不从心了。
- 传统RNN的突破:RNN通过在网络中添加“循环”结构,使得信息可以从一个步骤持久化到下一个步骤。这意味着它在处理序列中的第 $t$ 个元素时,会同时考虑当前的输入和来自处理第 $t-1$ 个元素时的“状态”(即记忆)。
- 核心结构与工作原理
- $x^{(t)}$: 在时间步 $t$ 的输入。例如,在句子中,它可能是一个单词的词向量。
- $h^{(t)}$:在时间步 $t$ 的隐藏状态。这就是RNN的“记忆”。它包含了之前所有时间步的汇总信息。
- $o^{(t)}$:在时间步 $t$ 的输出。例如,它可能是预测的下一个单词,或者当前单词的标签。
- 循环连接: 注意,从 $h^{(t-1)}$ 指向 $h^{(t)}$ 的箭头。这就是“循环”所在,它意味着当前的状态 $h^{(t)}$ 是由当前输入 $x^{(t)}$ 和前一状态 $h^{(t-1)}$ 共同计算得出的。
- $W$ 是权重矩阵,用于连接上一个隐藏状态 $h^{(t-1)}$。
- $U$ 是权重矩阵,用于连接当前输入 $x^{(t)}$。
- $b$ 是偏置项。
- $f$ 是激活函数,通常是 $\tanh$ 或 $\text{ReLU}$。$\tanh$ 能将输出值压缩到 (-1, 1) 之间,有助于稳定梯度。
- 传统RNN的优势
- 1. 处理变长序列: 无论输入序列是5个单词还是50个单词,同一个RNN单元都可以处理。
- 2. 参数共享: 在所有时间步上,模型参数$(U, W, V)$是共享的。这大大减少了需要学习的参数量,也使得模型可以泛化到不同长度的序列。
- 3. 捕捉时序依赖: 理论上,由于 $h^{(t)}$ 依赖于 $h^{(t-1)}$,而 $h^{(t-1)}$ 又依赖于 $h^{(t-2)}$,如此往复,RNN能够捕捉到序列中任意远距离的依赖关系。
- 应用场景
- 语言建模: 预测下一个字符或单词。
- 时间序列预测: 预测股票价格、天气等(短期趋势)。
- 简单的文本分类。
想象一下,当你阅读一个句子时,你并不会孤立地理解每一个单词。你会根据前面已经出现的单词来理解当前单词的含义。
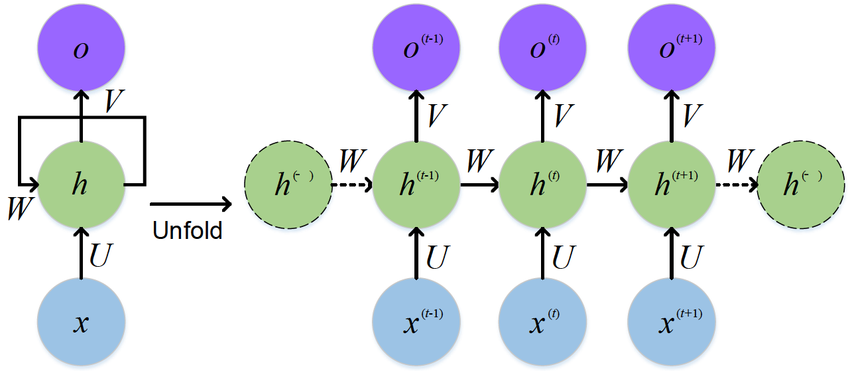
让我们来解读上面这个RNN的结构:
1. 循环单元展开
2.数学公式
$$ h^{(t)} = f(W\cdot h^{(t-1)} + U \cdot x^{(t)} + b)$$
其中:
输出$o^{(t)}$ 通常由 $h^{(t)}$ 经过一个简单的变换(比如一个全连接层和Softmax)得到:
$$ o^{(t)} = g(V \cdot h^{(t)} + c) $$
由于其简单的结构,传统RNN仍然可以用于一些短期依赖任务:
RNN计算
- 传统RNN单元
- 一个RNN单元可以有多个隐藏层吗?
- 一个RNN单元 = 一个隐藏层
- 多层RNN = 多个RNN单元堆叠
- 1. 标准设计:每个RNN单元是单层的
- 传统RNN: $h_t = \tanh(W_{hh}·h_{t-1} + W_{xh}·x_t + b_h)$ → 一次tanh
- LSTM: 多个门控计算,但每个门都是单层计算
- 2. 为什么通常不设计成多层?设计挑战:
- 实际的多层RNN实现方式:
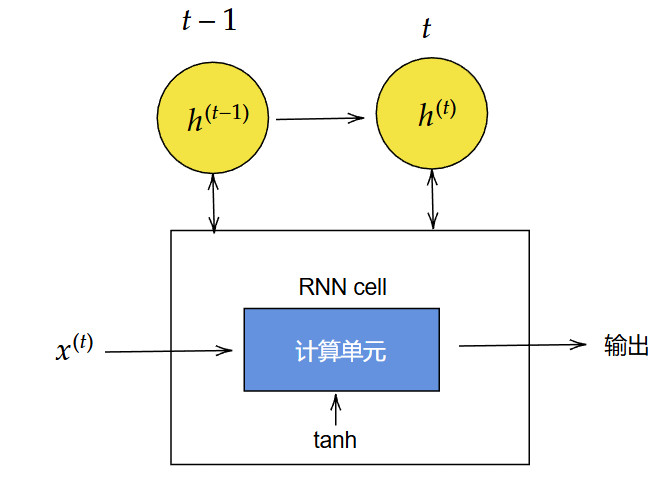
传统RNN单元的核心计算非常简单,只有三个步骤:
$$ z_t = W_{hh}h_{t-1} + W_{xh}x_t + b_h $$
$$ h_t = \tanh(z_t) $$
$$ o_t = \text{Sigmoid}(h_t) (可选) $$
其中$W_{hh}$表示$h_{(t-1)} \to h_{t}$之间的权重,$W_{xh}$表示$x \to h$之间的权重。
权重大小和参数数量:如果输入维度是$d_x$(若输入的是词向量,维度表明每个词用$d_x$维向量表示),隐藏层维度是$d_h$,那么:
$$ W_{xh}:d_h \times d_x $$
$$ W_{hh}:d_h \times d_h $$
$$ b_{h}:d_h $$
注意,权重矩阵的大小采用$d_h \times d_x$还是$d_x \times d_h$取决于在运算时权重矩阵在前还是在后,如果在后,应该是:$W_{xh}:d_x \times d_h$
在单个时间步的计算上,RNN单元等价于一个特殊的全连接层,其输入是[前一时间步的隐藏状态, 当前输入]的拼接。但在宏观上(整个序列处理、时间维度、状态保持),它是一个完全不同的、更强大的结构。但不能完全理解为一个全连接层,它们还是有很多不同之处:RNN单元:输出会作为下一时间步的输入,形成闭环、时间维度上的参数共享、处理变长序列的能力、状态持续性(记忆)等这些特征是全连接层不具备的。
首先必须澄清一个关键概念:一个RNN单元本身就是一个"层",而不是层中的组件。更准确地说:
这里的关键是:这个"单元"已经包含了完整的计算逻辑,它本身就是一个隐藏层。当人们问"一个RNN单元可以有多个隐藏层吗?",通常他们想问的是:一个RNN层内部是否可以有多层非线性变换?
答案:通常不这样设计,但有变体
在标准的RNN/LSTM/GRU中,每个单元内部的计算是一次非线性变换:
设计挑战:循环连接点不明确:应该从哪一层连接到下一时间步? 参数爆炸:如果每层都有循环连接,参数会急剧增加。训练困难:梯度需要在时间和深度两个维度传播。
在实践中,我们通过堆叠多个RNN单元来实现"深度",每个RNN单元都是单层的,但多个单元堆叠形成了深度。
一个简单的RNN计算举例
我们将判断一个长度为 3 的句子序列(用数字表示词向量)的情感是积极(输出 1)还是消极(输出 0)。这是一个多对一的RNN任务。
第一步:定义超参数和初始化参数
为了让计算简单明了,我们做以下假设:
符号说明
- $W$ 权重矩阵,用于连接上一个隐藏状态 $h_{t-1}$。
- $U$ 权重矩阵,用于连接当前输入 $x_t$。
- $V$ 权重矩阵,用于连接当前隐藏层 $h_t$。
- $b_h$ 隐藏层偏置项。
- $b_o$ 输出层偏置项。
初始化参数
$$\begin{array}{c}W=\begin{bmatrix}0.5&0.1\\ 0.2&0.8\\ \end{bmatrix}\\U=\begin{bmatrix}0.3&0.6\\ 0.9&0.4\\ \end{bmatrix}\\V=\begin{bmatrix}0.7\\ 0.5\\ \end{bmatrix}\\b_h=\begin{bmatrix}0.1&0.2\\ \end{bmatrix}\\b_o=0.3\end{array}$$
输入序列
$$\begin{bmatrix}1&0.5\\ 0.8&1\\ 0.2&0.9\\ \end{bmatrix}$$
初始隐藏状态
$$\begin{bmatrix}0&0\\ \end{bmatrix}$$
时间步: $t=$1
$$z_{1}=h_{0} \cdot W + x_{1} \cdot U + b_h$$
$$=\begin{bmatrix}0&0\\ \end{bmatrix} \cdot \begin{bmatrix}0.5&0.1\\ 0.2&0.8\\ \end{bmatrix} + \begin{bmatrix}1&0.5\\ \end{bmatrix} \cdot \begin{bmatrix}0.3&0.6\\ 0.9&0.4\\ \end{bmatrix} = \begin{bmatrix}0.85&1\\ \end{bmatrix}$$
$$h_{1}=\tanh(z_{1})=\begin{bmatrix}0.69107&0.76159\\ \end{bmatrix}$$
时间步: $t=$2
$$z_{2}=h_{1} \cdot W + x_{2} \cdot U + b_h$$
$$=\begin{bmatrix}0.69107&0.76159\\ \end{bmatrix} \cdot \begin{bmatrix}0.5&0.1\\ 0.2&0.8\\ \end{bmatrix} + \begin{bmatrix}0.8&1\\ \end{bmatrix} \cdot \begin{bmatrix}0.3&0.6\\ 0.9&0.4\\ \end{bmatrix} = \begin{bmatrix}1.73785&1.75838\\ \end{bmatrix}$$
$$h_{2}=\tanh(z_{2})=\begin{bmatrix}0.93998&0.94232\\ \end{bmatrix}$$
时间步: $t=$3
$$z_{3}=h_{2} \cdot W + x_{3} \cdot U + b_h$$
$$=\begin{bmatrix}0.93998&0.94232\\ \end{bmatrix} \cdot \begin{bmatrix}0.5&0.1\\ 0.2&0.8\\ \end{bmatrix} + \begin{bmatrix}0.2&0.9\\ \end{bmatrix} \cdot \begin{bmatrix}0.3&0.6\\ 0.9&0.4\\ \end{bmatrix} = \begin{bmatrix}1.62845&1.52786\\ \end{bmatrix}$$
$$h_{3}=\tanh(z_{3})=\begin{bmatrix}0.92584&0.91006\\ \end{bmatrix}$$
最终输出
$$o_{3}=V \cdot h_{3} + b_o =\begin{bmatrix}0.7\\ 0.5\\ \end{bmatrix}\cdot \begin{bmatrix}0.92584&0.91006\\ \end{bmatrix}+0.3=1.40312$$
$$ y_3 = \text{sigmoid}(o_3) \approx 0.803 $$
结果解释:
我们的最终输出 $y_3 ≈ 0.803$由于我们使用的是 sigmoid 激活函数,输出值在 0 到 1 之间。我们可以设置一个阈值(比如 0.5): 如果 $y_3 > 0.5$,则预测为积极(1),如果 $y_3 \leq 0.5$,则预测为消极(0),在这个例子中,0.803 > 0.5,所以RNN模型预测这个句子的情感是积极的。
RNN反向传播
一、 问题定义与符号说明
考虑一个简单的单层RNN,做多对一分类任务(如情感分析):
- 时间步:$t=1,2,\cdots , T$
- 输入序列:$x_1,x_2,\cdots, x_T$
- 隐藏状态:$h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h)$
- 输出层:$o = W_{hy}h_T + b_y$(仅用最后时刻的$h_T$)
- 预测输出:$\hat{y} = \text{softmax}(o)$
其中,$W_{hy}$是隐藏层→输出层的权重矩阵,$b_y$输出层的偏置。$W_{hh}$是隐藏层的权重,$b_h$是隐藏层的偏置。$W_{xh}$是输入至隐藏层的权重。
损失函数:交叉熵损失
$$ L = - \sum_{k=1}^K y_k\log(\hat{y}_k)$$其中$K$是类别数。输出层梯度的计算遵循标准的反向传播思想,但由于RNN只在最后时间步使用输出层,计算相对简单。
其中$$\hat{y}_k = \frac{e^{o_k}}{ \displaystyle{ \sum_{j=1}^K e^{o_j}}} $$
计算损失对输出层的权重梯度,与反向传播的算法相似,对于交叉熵损失函数,它的梯度计算如下:
$$ \frac{\partial L}{\partial o_i} = \hat{y}_i - y_i $$
$$ \frac{\partial L}{\partial W_{hy}} = (\hat{y} - y)\cdot h_T^T $$
$$ \frac{\partial L}{\partial b_{y}} = \hat{y} - y $$
二、 时间反向传播(BPTT)
时间反向传播 本质上是标准反向传播在时间维度上的扩展。核心挑战在于:RNN的参数在所有时间步共享,因此损失函数对某个参数的梯度需要累加所有时间步的贡献。在BPTT中,我们将RNN在时间上展开成一个深度前馈网络,然后应用标准反向传播。但有一个重要区别:共享权重意味着梯度要跨时间步累积。
前向传播方程:
- 1. 隐藏层:
- $h_t$ : 时间步t的隐藏状态
- $W_{hh}$:隐藏层到隐藏层权重
- $W_{xh}$:输入到隐藏层权重
- $b_h$:隐藏层偏置
- 2. 输出层
- 3. 损失函数(交叉熵)
$$ h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_h) $$
$$ o = W_{hy}h_T + b_y $$
$$ \hat{y} = \text{softmax}(o)$$
$$ L = -\sum_{k=1}^Ky_k\log(\hat{y}_k)$$
三、 BPTT 详细推导
我们将计算$L$对$W_{hh}$和$W_{xh}$的梯度。这是BPTT的核心。
步骤1:定义局部导数
隐藏层净输入:$$ z_t=W_{hh}h_{t-1} + W_{xh}x_t + b_h $$
隐藏层激活:$$ h_t=\tanh(z_t) $$
导数关系
$$ \frac{\partial h_t}{\partial z_t} = \text{diag}(1-h_t \odot h_t)$$(tanh的导数)
$$ \frac{\partial z_t}{\partial h_{t-1}} = W_{hh}^T $$
$$ \frac{\partial z_t}{\partial W_{hh}} = h_{t-1}^T $$
步骤2:计算损失对$h_t$的梯度
这是BPTT的关键步骤。损失 $L$通过所有后续的时间步影响$h_t$:
设$\delta_t=\frac{\partial L}{\partial z_t}$为损失对净输入$z_t$的梯度。从最后一个时间步 $T$ 开始反向计算:
情况1:$t=T$(最后一个时间步),损失直接影响$h_T$
$$ \frac{\partial L}{\partial h_T} = W_{hy}^T \cdot \frac{\partial L}{\partial o} $$其中$\frac{\partial L}{\partial o} = \hat{y} - y$(来自输出层梯度)
$$ \delta_T = \frac{\partial L}{\partial z_T} = \frac{\partial L}{\partial h_T} \odot (1-h_T\odot h_T)$$这里$\odot$表示逐元素相乘。
情况2:$t < T$(中间时间步):$h_T$通过两条路径影响损失,对于多对一任务(只有最后时间步有输出):
$$ \frac{\partial L}{\partial h_t} = \frac{\partial z_{t+1}}{\partial h_t} \cdot \frac{\partial L}{\partial z_{t+1}} = W_{hh}^T \cdot \delta_{t+1} $$
$$ \delta_{t} = \frac{\partial L}{\partial z_t} = \frac{\partial L}{\partial h_t} \odot (1-h_t \odot h_t)$$
$$ \delta_{t} = (W_{hh}^T\cdot \delta_{t+1}) \odot (1-h_t \odot h_t)$$
步骤3:计算对权重的梯度
对$W_{hh}$的梯度
由于$W_{hh}$出现在每个时间步,梯度是所有时间步贡献之和:
$$ \frac{\partial L}{\partial W_{hh}} = \sum_{t=1}^T \frac{\partial L}{\partial z_t} \cdot \frac{\partial z_t}{\partial W_{hh}} = \sum_{t=1}^T \delta_t \cdot h_{t-1}^T $$
对$W_{xh}$的梯度
$$ \frac{\partial L}{\partial W_{xh}} = \sum_{t=1}^T \frac{\partial L}{\partial z_t} \cdot \frac{\partial z_t}{\partial W_{xh}} = \sum_{t=1}^T \delta_t \cdot x_{t}^T $$
对$b_{h}$的梯度
$$ \frac{\partial L}{\partial b_{h}} = \sum_{t=1}^T \frac{\partial L}{\partial z_t} = \sum_{t=1}^T \delta_t $$
在QkCalc中设计RNN
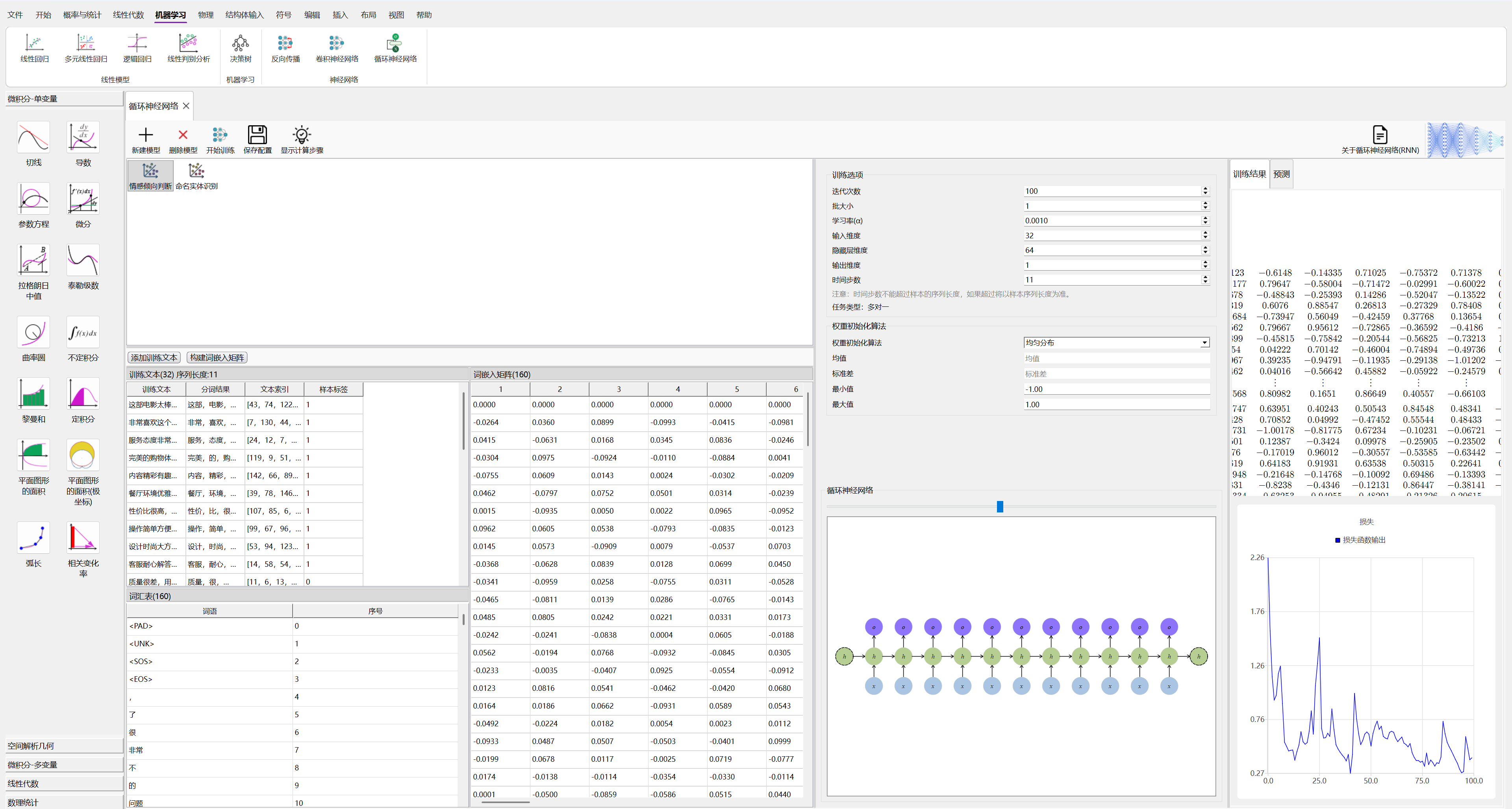
在QkCalc中,你可以通过“循环神经网络”来建立有关RNN的模型,在该模块中,你可以建立不同类型的RNN网络,生成样本词嵌入矩阵进行训练,查看训练结果和进行预测。
